La loi d’Ohms
La loi et le pouvoir d’Ohms

En connaissant deux valeurs quelconques de la tension, du courant ou de la résistance, nous pouvons utiliser la loi d’Ohms pour trouver la troisième valeur manquante. La loi d’Ohms est largement utilisée dans les formules et les calculs électroniques, il est donc » très important de comprendre et de se souvenir précisément de ces formules « .
Pour trouver la tension, ( V)
V = [ I x R ] V (volts) = I (ampères) x R (Ω)
Pour trouver le courant, ( I)
I = [ V ÷ R ] I (ampères) = V (volts) ÷ R (Ω)
Pour trouver la résistance, ( R)
R = [ V ÷ I ] R (Ω) = V (volts) ÷ I (ampères)
Il est parfois plus facile de se souvenir de cette relation juridique d’Ohms en utilisant des images. Ici, les trois grandeurs de V, I et R ont été superposées en un triangle (affectueusement appelé le triangle de la loi d’Ohms) donnant la tension au sommet avec courant et résistance en dessous. Cet arrangement représente la position réelle de chaque quantité dans les formules de la loi Ohms.
Ohms Triangle de la loi

La transposition de l’équation standard de la loi d’Ohms ci-dessus nous donnera les combinaisons suivantes de la même équation :

Ensuite, en utilisant la loi d’Ohms, nous pouvons voir qu’une tension de 1V appliquée à une résistance de 1Ω fera passer un courant de 1A et plus la valeur de résistance est élevée, moins le courant circulera pour une tension appliquée donnée. Tout appareil ou composant électrique qui obéit à la loi d’Ohms, c’est-à-dire que le courant qui le traverse est proportionnel à la tension qui le traverse ( I α V), comme les résistances ou les câbles, sont dits de nature « ohmique », et les appareils qui ne le sont pas, comme les transistors ou les diodes, sont considérés comme des appareils « non ohmiques ».
Puissance électrique dans les circuits
L’énergie électrique () dans un circuit est la vitesse à laquelle l’énergie est absorbée ou produite à l’intérieur d’un circuit. Une source d’énergie telle qu’une tension produira ou délivrera de l’énergie pendant que la charge connectée l’absorbe. Les ampoules et les appareils de chauffage, par exemple, absorbent l’énergie électrique et la convertissent soit en chaleur, soit en lumière, soit les deux. Plus leur valeur ou leur puissance nominale en watts est élevée, plus ils sont susceptibles de consommer de l’énergie électrique.
Le symbole de quantité pour la puissance est P et est le produit de la tension multipliée par le courant, l’unité de mesure étant le Watt ( » W « ). Les préfixes sont utilisés pour désigner les différents multiples ou sous-multiples d’un watt, tels que : milliwatts (mW = 10-3W) ou kilowatts (kW = 103W).
Ensuite, en utilisant la loi d’Ohm et en substituant aux valeurs de V, I et R la formule pour la puissance électrique peut être trouvée comme :
Pour trouver la puissance (P)
P = V x I ] P (watts) = V (volts) x I (ampères)
Aussi :
P = V2 ÷ R ] P (watts) = V2 (volts) ÷ R (Ω)
Aussi :
P = I2 x R ] P (watts) = I2 (ampères) x R (Ω)
Encore une fois, les trois grandeurs ont été superposées dans un triangle appelé cette fois un triangle de puissance avec la puissance en haut et le courant et la tension en bas. Encore une fois, cet arrangement représente la position réelle de chaque quantité dans les formules de puissance de la loi d’Ohms.
Le triangle de la puissance

et encore une fois, la transposition de l’équation de base de la loi d’Ohms ci-dessus pour la puissance nous donne les combinaisons suivantes de la même équation pour trouver les différentes grandeurs individuelles :

Nous pouvons donc voir qu’il existe trois formules possibles pour calculer la puissance électrique d’un circuit. Si la puissance calculée est positive, (+P) en valeur pour n’importe quelle formule, le composant absorbe la puissance, c’est-à-dire qu’il consomme ou utilise la puissance. Mais si la puissance calculée est négative, (-P) en valeur, le composant produit ou génère de l’énergie, en d’autres termes, il est une source d’énergie électrique comme les batteries et les générateurs.
Puissance électrique nominale
Les composants électriques reçoivent une « puissance nominale » en watts qui indique la vitesse maximale à laquelle le composant convertit l’énergie électrique en d’autres formes d’énergie telles que la chaleur, la lumière ou le mouvement. Par exemple, une résistance 1/4W, une ampoule de 100W, etc.
Les appareils électriques convertissent une forme d’énergie en une autre. Ainsi, par exemple, un moteur électrique transformera l’énergie électrique en une force mécanique, tandis qu’un générateur électrique convertira la force mécanique en énergie électrique. Une ampoule transforme l’énergie électrique en lumière et en chaleur.
De plus, nous savons maintenant que l’unité de puissance est le WATT, mais certains appareils électriques comme les moteurs électriques ont une puissance nominale dans l’ancienne mesure de la « puissance en chevaux » ou hp. La relation entre la puissance et le nombre de watts est donnée sous la forme : 1 ch = 746 W. Ainsi, par exemple, un moteur de deux chevaux-vapeur a une puissance nominale de 1492W, (2 x 746) ou 1,5kW.
Diagramme circulaire sur la loi Ohms
Pour nous aider à mieux comprendre la relation entre les différentes valeurs, nous pouvons prendre toutes les équations de la loi d’Ohm par le haut pour trouver la tension, le courant, la résistance et bien sûr la puissance et les condenser dans un simple diagramme circulaire de la loi d’Ohms pour les circuits et calculs AC et DC comme indiqué.
Diagramme circulaire sur la loi Ohms

En plus d’utiliser le diagramme circulaire de la loi d’Ohm illustré ci-dessus, nous pouvons également placer les équations individuelles de la loi d’Ohm dans un tableau matriciel simple, comme indiqué pour faciliter le calcul d’une valeur inconnue.
Tableau de la matrice des lois d’Ohms

Exemple de loi Ohms No1
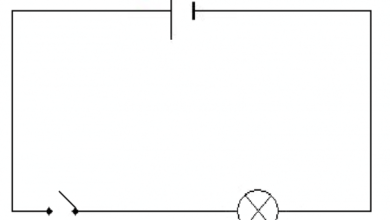
Pour le circuit illustré ci-dessous, trouvez la tension (V), le courant (I), la résistance (R) et la puissance (P).

Tension [ V = I x R ] = 2 x 12Ω = 24V
Courant [ I = V ÷ R ] = 24 ÷ 12Ω = 2A
Résistance [ R = V ÷ I ] = 24 ÷ 2 = 12 Ω
Puissance [ P = V x I ] = 24 x 2 = 48W
L’alimentation d’un circuit électrique n’est présente que lorsque les DEUX tensions et courants sont présents. Par exemple, en condition de court-circuit, la tension est présente mais il n’y a pas de courant I = 0 (zéro), donc V*0 est 0, donc la puissance dissipée dans le circuit doit aussi être 0. De même, si nous avons un court-circuit, le courant est présent mais il n’y a aucune tension V = 0, donc 0*I = 0, la puissance dissipée dans le circuit est de nouveau 0.
Comme l’énergie électrique est le produit de V*I, la puissance dissipée dans un circuit est la même, que le circuit contienne une haute tension et un courant faible ou une basse tension et un courant élevé. Généralement, l’énergie électrique est dissipée sous forme de chaleur (appareils de chauffage), de travaux mécaniques comme les moteurs, d’énergie sous forme de rayonnement (lampes) ou d’énergie stockée (batteries).
L’énergie électrique dans les circuits
L’énergie électrique est la capacité d’effectuer un travail, et l’unité de travail ou d’énergie est le joule ( J). L’énergie électrique est le produit de la puissance multipliée par la durée de sa consommation. Donc, si nous savons combien d’énergie, en watts, est consommée et le temps, en secondes, pour lequel elle est utilisée, nous pouvons trouver l’énergie totale utilisée en watts-secondes. En d’autres termes, Energie = puissance x temps et Puissance = tension x courant. Par conséquent, la puissance électrique est liée à l’énergie et l’unité donnée pour l’énergie électrique est le watt-seconde ou le joule.
![]()
L’énergie électrique peut également être définie comme la vitesse à laquelle l’énergie est transférée. Si un joule de travail est absorbé ou délivré à une vitesse constante d’une seconde, la puissance correspondante sera équivalente à un watt, de sorte que la puissance peut être définie comme « 1Joule/sec = 1Watt ». On peut alors dire qu’un watt est égal à un joule par seconde et que la puissance électrique peut être définie comme la vitesse de travail ou le transfert d’énergie.
Triangle de l’énergie et de l’énergie électrique

ou pour trouver les différentes quantités individuelles :

Nous avons dit précédemment que l’énergie électrique est définie comme étant le nombre de watts par seconde ou joules. Bien que l’énergie électrique soit mesurée en Joules, elle peut devenir une valeur très importante lorsqu’elle est utilisée pour calculer l’énergie consommée par un composant.
Par exemple, si une ampoule de 100 watts est laissée allumée pendant 24 heures, l’énergie consommée sera de 8 640 000 Joules (100 W x 86 400 secondes), donc des préfixes tels que kilojoules (kJ = 103J) ou mégajoules (MJ = 106J) sont utilisés à la place et dans cet exemple simple, l’énergie consommée sera 8,64 MJ (méga-Joules).
Mais s’agissant des joules, des kilojoules ou des mégajoules pour exprimer l’énergie électrique, les mathématiques impliquées peuvent se retrouver avec de grands nombres et beaucoup de zéros, il est donc beaucoup plus facile d’exprimer l’énergie électrique consommée en Kilowattheures.
Si la puissance électrique consommée (ou produite) est mesurée en watts ou en kilowatts (milliers de watts) et que le temps est mesuré en heures et non en secondes, alors l’unité d’énergie électrique sera le kilowattheure (kWhr). Alors notre ampoule de 100 watts ci-dessus consommera 2 400 watts-heure ou 2,4kWhr, ce qui est beaucoup plus facile à comprendre avec les 8 640 000 joules.
1 kWh est la quantité d’électricité consommée par un appareil d’une puissance nominale de 1000 watts en une heure et est communément appelée « unité d’électricité ». C’est ce qui est mesuré par le compteur du service public et c’est ce que nous, en tant que consommateurs, achetons à nos fournisseurs d’électricité lorsque nous recevons nos factures.
Les kilowattheures sont les unités d’énergie standard utilisées par le compteur d’électricité de nos maisons pour calculer la quantité d’énergie électrique que nous utilisons et donc combien nous payons. Ainsi, si vous allumez un feu électrique avec un élément chauffant de 1000 watts et que vous le laissez allumé pendant 1 heure, vous aurez consommé 1 kWh d’électricité. Si vous allumez deux feux électriques de 1000 watts chacun pendant une demi-heure, la consommation totale serait exactement la même quantité d’électricité – 1kWhr.
Ainsi, une consommation de 1000 watts pendant une heure consomme la même quantité d’énergie que 2000 watts (deux fois plus) pendant une demi-heure (la moitié du temps). Ensuite, pour qu’une ampoule de 100 watts utilise 1 kWh ou une unité d’énergie électrique, il faudrait l’allumer pendant 10 heures au total (10 x 100 = 1000 = 1kWhr).
Maintenant que nous connaissons la relation entre la tension, le courant et la résistance dans un circuit, dans le prochain tutoriel relatif aux circuits CC, nous allons examiner les unités électriques standard utilisées en génie électrique et électronique pour nous permettre de calculer ces valeurs et voir que chaque valeur peut être représentée par des multiples ou sous-multiples de l’unité standard.
David Schmidt