Analyse du courant de maille

L’analyse du courant de maille est une technique utilisée pour trouver les courants circulant autour d’une boucle ou d’un maillage dans n’importe quel circuit fermé d’un circuit.

Tandis que Kirchhoff´s Les lois nous donnent la méthode de base pour analyser n’importe quel circuit électrique complexe, il y a différentes manières d’améliorer cette méthode en utilisant l’analyse de courant de maille ou l’analyse de tension nodale qui a comme conséquence une diminution des mathématiques impliquées et quand
Circuit d’analyse de courant de maille

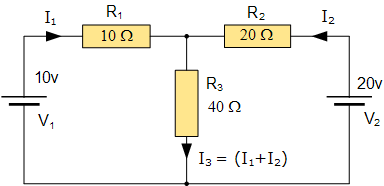
Une méthode simple pour réduire la quantité de mathématiques impliquées est d’analyser le circuit en utilisant les équations de loi de courant de Kirchhoff pour déterminer les courants, I1 et I2 circulant dans les deux résistances. Il n’est donc pas nécessaire de calculer l’I3 actuel comme étant simplement la somme de I1 et I2. Ainsi, la deuxième loi de tension de Kirchhoff devient tout simplement :

Équation no 1 : 10 = 50I1 + 40I2
Équation no 2 : 20 = 40I1 + 60I2

par conséquent, une ligne de calcul mathématique a été sauvegardée.
Analyse du courant de maille

Une méthode plus facile pour résoudre le circuit ci-dessus est d’utiliser l’analyse du courant de maille ou l’analyse de boucle qui est aussi parfois appelée Maxwell´s La méthode des courants de circulation. Au lieu d’étiqueter les courants de dérivation, nous devons étiqueter chaque « boucle fermée » avec un courant circulant.

En règle générale, n’étiqueter qu’à l’intérieur des boucles dans le sens des aiguilles d’une montre avec les courants circulant, car le but est de couvrir tous les éléments du circuit au moins une fois. Tous les courants de dérivation nécessaires peuvent être trouvés à partir de la boucle appropriée ou des courants de maille comme avant en utilisant la méthode Kirchhoff´s méthode.

Par exemple : : i1 = I1, i2 = -I2 et I3 = I1 – I2

Nous écrivons maintenant l’équation de Kirchhoff de la loi de tension de la même manière qu’auparavant pour les résoudre, mais l’avantage de cette méthode est qu’elle garantit que l’information obtenue à partir des équations de circuit est le minimum requis pour résoudre le circuit car l’information est plus générale et peut facilement être mise sous forme de matrice.

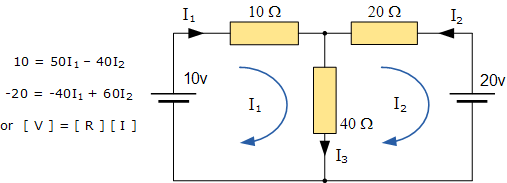
Ces équations peuvent être résolues assez rapidement en utilisant une seule matrice d’impédance de maille Z. Chaque élément sur la diagonale principale sera « positif » et est l’impédance totale de chaque maille. Où as, chaque élément OFF, la diagonale principale sera soit « zéro » soit « négative » et représente l’élément de circuit reliant toutes les mailles appropriées.

Tout d’abord, nous devons comprendre que lorsqu’il s’agit de matrices, pour la division de deux matrices, c’est la même chose que la multiplication d’une matrice par l’inverse de l’autre, comme indiqué.

Matrice de courant de maille ayant trouvé l’inverse de R, puisque V/R est le même que V x R-1, on peut maintenant l’utiliser pour trouver les deux courants en circulation.

analyse du courant de maillage du circuit

Où :

V ] donne la tension totale de la batterie pour la boucle 1 puis la boucle 2
I ] indique les noms des courants de boucle que nous essayons de trouver
R ] est la matrice de résistance
R-1 ] est l’inverse de la matrice [ R ].

et cela donne I1 à -0,143 A et I2 à -0,429 A.

Comme : I3 = I1 – I2

Le courant combiné de I3 est donc donné comme : -0,143 – (-0,429) = 0,286 A

qui est la même valeur de 0.286 ampères, que nous avons trouvé en utilisant la loi de circuit Kirchoff´s dans le tutoriel précédent.
Résumé de l’analyse des courants de maille

Cette méthode d’analyse de circuit « look-see » est probablement la meilleure de toutes les méthodes d’analyse de circuit avec la procédure de base pour résoudre les équations Mesh Current Analysis est la suivante :

1. Marquer toutes les boucles internes avec des courants circulants. (I1, I2, …IL etc)
2. Ecrire la matrice de colonnes [ L x 1 ] [ V ] donnant la somme de toutes les sources de tension dans chaque boucle.
3. Ecrire la matrice [ L x L ], [ R ] pour toutes les résistances du circuit comme suit :
R11 = la résistance totale dans la première boucle.
Rnn = la résistance totale dans la boucle N.
RJK = la résistance qui relie directement la boucle J à la boucle K.
4. Ecrire la matrice ou l’équation vectorielle[V] =[R] x[I] où[I] est la liste des courants à trouver.

En plus de l’analyse du courant de maille, nous pouvons aussi utiliser l’analyse des nœuds pour calculer les tensions autour des boucles, ce qui réduit encore une fois la quantité de mathématiques nécessaires en utilisant uniquement les lois de Kirchoff. Dans le prochain tutoriel relatif à la théorie des circuits CC, nous nous pencherons sur l’analyse de tension nodale pour y parvenir.

David Schmidt